Feladat: Összeadás [*]
Definiáljuk az összeadást:
Segítség:
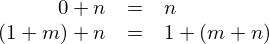
A következő algebrai adatszerkezet rekurzív:
Definiáljuk a következő konstansokat:
Definiáljuk az összeadást:
Segítség:
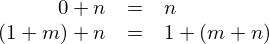
Definiáljuk a szorzást:
Segítség:
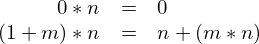
Definiáljuk a pozitív bináris számokat! Egy pozitív bináris szám
Definiáljuk a bináris számok jelentését!
A Preludben a speciális szintaxistól eltekintve így lehetne definiálni:
Definiáljunk egy bináris fa adatszerkezetet, ami a csomópontokban adatot tartalmaz!