Feladat: Polinom kiértékelése
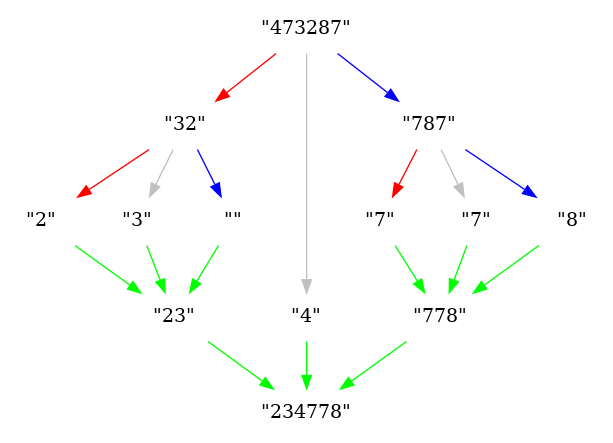
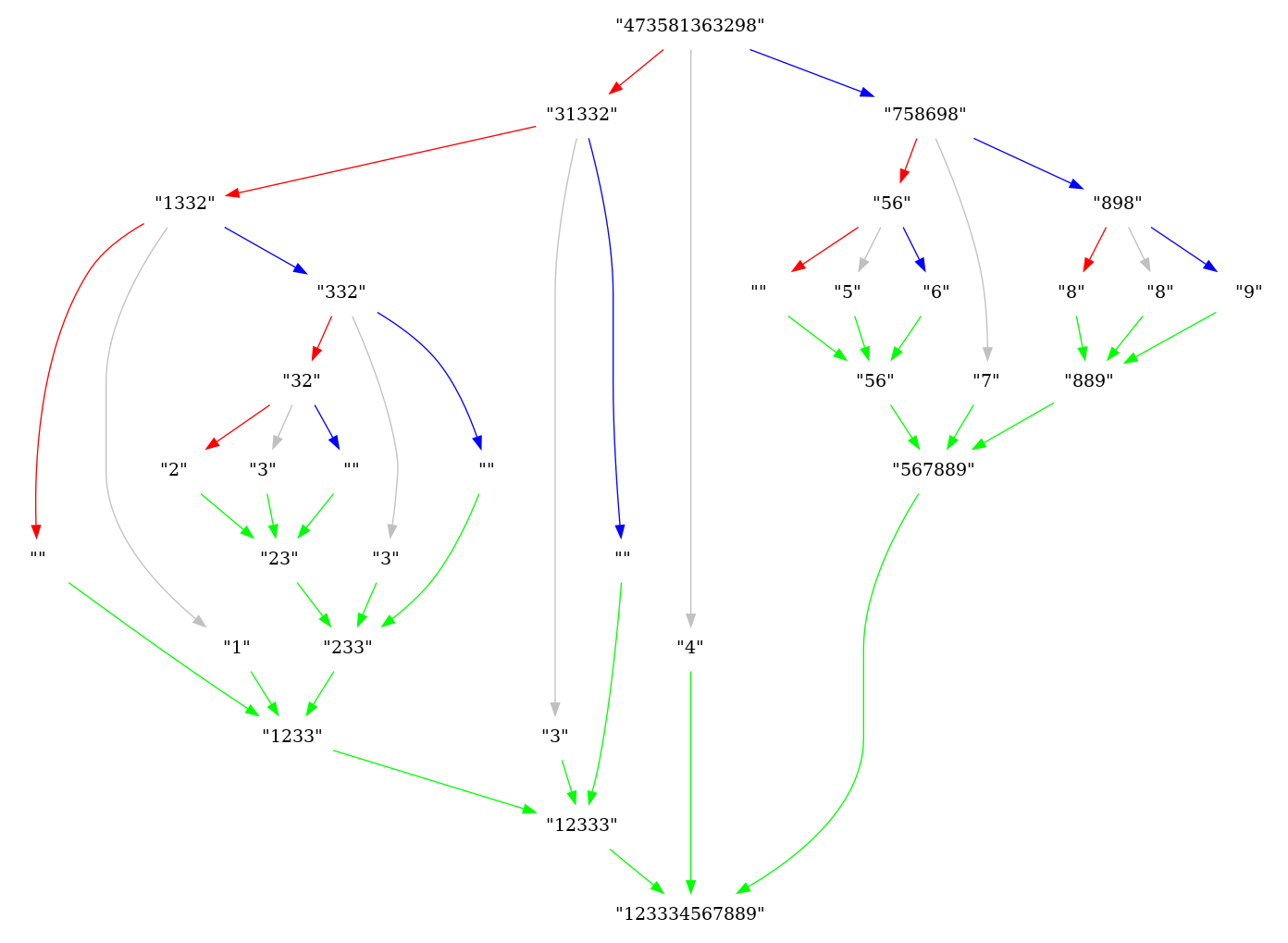
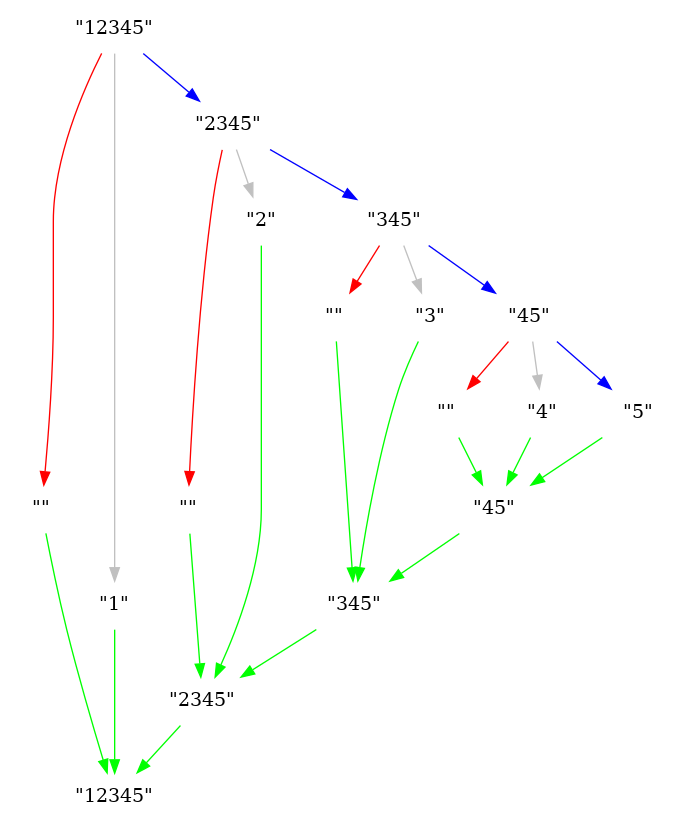
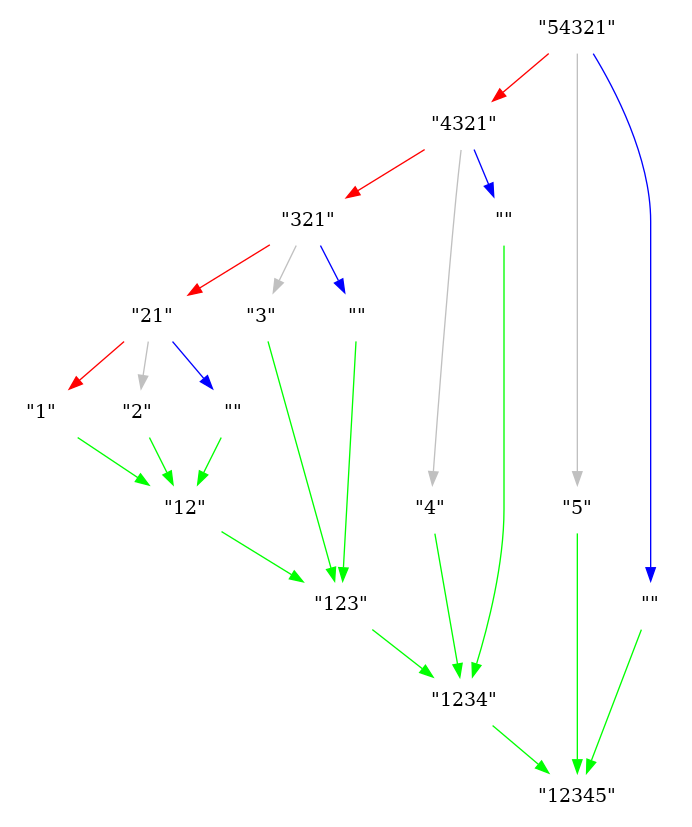
Értékeljünk ki adott helyen egy együtthatóival megadott polinomot! A számítás alapját a Horner-séma képzi, amelynek megfelelően a polinom általános alakja:
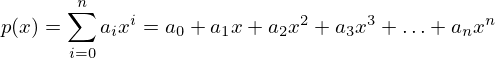
átírható (a számítás szempontjából kedvezőbb) monomiális formára:
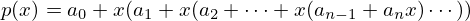
Ügyeljünk arra, hogy a polinom együtthatói a listában fordított sorrendben szerepelnek, hogy a rekurziót könnyebb legyen felírni.