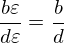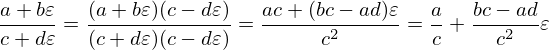Számolás mátrixokkal és gyors hatványozással
A fib2 függvény egyetlen lépése:
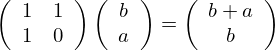
Ebből:
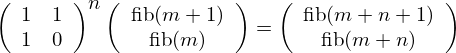
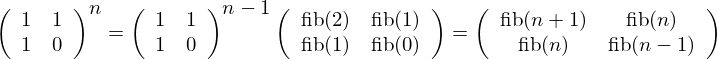
Azonosság vizsgálat:
Num osztályNum példány(+), (*), fromInteger metódusokNum osztályPéldányosítsuk a Num osztályt a Peano számokra.
Definiáljuk csak a (+), (*), fromInteger metódusokat.
Num példányPéldányosítsuk a Num osztályt a Nat2 típusra.
Definiáljuk csak a (+), (*), fromInteger metódusokat.
instance Num Nat2 where
fromInteger 1 = One
fromInteger n = (if even n then D else SD) $ fromInteger $ n `div` 2
One + m = s m
n + One = s n
D n + D m = D (n + m) -- 2*n + 2*m = 2*(n+m)
SD n + D m = SD (n + m) -- 2*n+1 + 2*m = 2*(n+m)+1
D n + SD m = SD (n + m) -- 2*n + 2*m+1 = 2*(n+m)+1
SD n + SD m = D (s (n + m))-- 2*n+1 + 2*m+1 = 2*(1+n+m)+1
One * m = m
D n * m = D (n*m) -- 2*n * m = 2*(n*m)
SD n * m = D (n*m) + m -- (2*n+1) * m = 2*(n*m) + m
abs = undefined
signum = undefined
negate = undefined
-- mintaillesztés, rekurziósqr :: Nat2 -> Nat2 -- négyzetreemelés
sqr One = One
sqr (D n) = D (D (sqr n)) -- (2*n)^2 = 2*2*n^2
sqr (SD n) = SD (D (n + sqr n)) -- (2*n+1)^2 = 2*(2*(n + n^2))+12*2-es mátrixok ===============
(+), (*), fromInteger metódusokinstance Num a => Num (Mat2x2 a) where
Mat2x2 a b c d + Mat2x2 a' b' c' d'
= Mat2x2 (a+a') (b+b') (c+c') (d+d')
Mat2x2 a b
c d * Mat2x2 a' b'
c' d'
= Mat2x2 (a*a'+b*c') (a*b'+b*d')
(c*a'+d*c') (c*b'+d*d')
fromInteger n = Mat2x2 (fromInteger n) 0
0 (fromInteger n)
abs = undefined
signum = undefined
negate = undefined
-- mintaillesztésLassú definíció (exponenciális):
Gyorsabb (lineáris):
Ezek azonosak:
A következő definícióban az elvégzett alapműveletek száma O(log(n)).
A fib2 függvény egyetlen lépése:
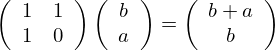
Ebből:
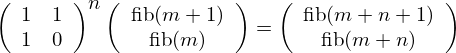
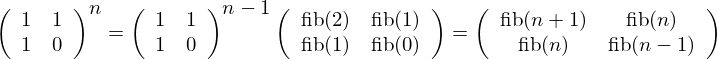
Azonosság vizsgálat:
A duális számok a + bε alakú számok, ahol ε2=0.
Reprezentáljuk az a + bε számot a Dual a b értékkel:
Definiáljuk a (+), (-), (*), fromInteger metódusokat.
instance (Num a) => Num (Dual a) where
Dual a b + Dual c d = Dual (a + c) (b + d)
-- (a + b*ε) + (c + d*ε) = (a+c) + (b+d)*ε
Dual a b - Dual c d = Dual (a - c) (b - d)
-- (a + b*ε) - (c + d*ε) = (a-c) + (b-d)*ε
Dual a b * Dual c d = Dual (a * c) (a * d + b * c)
-- (a + b*ε) * (c + d*ε) = (a*c) + (a*d+b*c)*ε
abs = undefined
signum = undefined
fromInteger n = Dual (fromInteger n) 0A Fractional osztály:
Példányosítsuk Fractional-t Mat2x2-re.
instance Fractional a => Fractional (Mat2x2 a) where
fromRational r = Mat2x2 (fromRational r) 0
0 (fromRational r)
recip (Mat2x2 a b c d) = Mat2x2 (m*d) (-m*b) (-m*c) (m*a) where
m = 1/(a*d-b*c)
-- lásd a következő képletet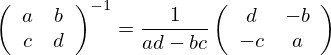
fastFib' :: Int -> Integer
fastFib' n = numerator x where
(Mat2x2 _ x _ _)
= Mat2x2 1 1 1 0 ^^ n :: Mat2x2 RationalPélda:
Felhasznált függvények:
Példányosítsuk Fractional-t Dual-ra.
instance (Eq a, Fractional a) => Fractional (Dual a) where
fromRational r = Dual (fromRational r) 0
Dual 0 a / Dual 0 b = Dual (a/b) 0
Dual a b / Dual c d = Dual (a/c) ((b*c-a*d)/c^2)
-- ...