Feladatok
Zárójelezés (2 pont)
Adjuk meg az alábbi kifejezés teljes és helyes zárójelezését!
Távolítsuk el a következő kifejezésből a lehető legtöbb zárójelpárt úgy, hogy a kifejezés megőrizze a jelenlegi jelentését!
Locsolási terv (1 pont)
Kata előszeretettel segít az édesanyjának a kerti munkákban. Feladatként azt kapta, hogy locsolja meg a virágokat.
A virágok egy nagy ládában találhatóak, összesen 50 tő. Egy tő virágnak legalább negyed liter vízre van szüksége. Katának egy 1.8 literes öntözőkannája van.
Adjuk meg azt a kifejezést, amely kiszámolja Katának, hogy hány alkalommal kell vizet töltenie az öntözőkannába (az eredmény tehát egy egész szám)!
Megjegyzés:
- Az eredménynek egész típusú értéknek kell lennie!
Függvényérték (2 pont)
Melyik az a legkisebb x egész szám, amely esetén az f(x) értéke nagyobb mint 1000? Adjuk meg azt a kifejezést, amely kiszámolja ezt!
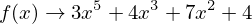
Eredő ellenállás számítás (2 pont)
Gábornak 50 és 250 között egyesével növekvő, egész értékű Ω-os ellenállása van (R). Mindegyik ellenállásból pontosan egy darab áll a rendelkezésére.
Segítsünk Gábornak és adjuk meg azt a két kifejezést, amely segítségével könnyedén meghatározhatja az eredő ellenállás értékét soros, illetve párhuzamos kapcsolása esetén!
Sorosan kapcsolva az ellenállást az alábbi kifejezéssel határozhatjuk meg:
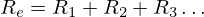
Párhuzamosan kapcsolva az ellenállást az alábbi kifejezéssel határozhatjuk meg:
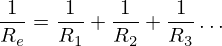
Barátságos számpárok (2 pont)
Azokat a számpárokat, amelyekre igaz, hogy az egyik szám önmagánál kisebb osztóinak összege a másik számmal egyenlő és fordítva, barátságos számoknak hívjuk.
- Adjuk meg azt a kifejezést, amely előállítja a 220 önmagánál kisebb egész osztóinak összegét! Adjuk meg ugyanezt a kifejezést a 284-re is!
- Adjuk meg azt a logikai kifejezést, amely az a) pontban megadott kifejezések felhasználásával eldönti, hogy a 220 és a 284 barátságos számpárt alkot-e! Amennyiben barátságos számpárt alkotnak, úgy a kifejezés értéke legyen
True, ellenkező esetbenFalse.
Számok és osztóik (3 pont)
Állíts elő egy olyan rendezett párokból álló listát, amelyben szerepel az első 50 pozitív egész szám és a szám osztói!
Az eredmény lista típusa [(Int, [Int])] legyen, ahol a pár első eleme a pozitív egész szám, második eleme pedig a szám osztóinak listája.
Például:
[(1,[1]),(2,[1,2]),(3,[1,3]),(4,[1,2,4]),(5,[1,5]) ...]
Pitagoraszi számhármasok (3 pont)
Keressük meg azokat a Pitagoraszi számhármasokat, melyek összege 150. Pitagoraszi számhármasnak nevezzük azt a (a, b, c) hármast, melyre a2 + b2 = c2 teljesül. (Tipp: c-t fejezzük ki a-val és b-vel.)