A feladat összefoglaló leírása
A feladatban a Floyd-Warshall algoritmus megvalósításával fogunk foglalkozni, amelyet élsúlyozott gráfok legrövidebb útjainak keresésére használnak.
Az általunk definiált függvények megadják a távolság- és az útvonalgráfot. A távolság gráf segítségével a gráf két tetszőleges pontja közötti legrövidebb (legkevésbé költséges) út összköltségét, az útvonalgráffal pedig megadható ezen legrövidebb útvonal.
A bemeneti gráfban irányított éleket tartalmaz és az élek súlyai tetszőleges egész értékek lehetnek. A gráffal szemben megköveteljük, hogy ne legyen benne egyetlen negatív összköltségű út sem.
A feladatunk, hogy egy élsúlyozott, irányított és negatív összköltségű irányított kört nem tartalmazó véges gráf tetszőleges u, v csúcspárjára meghatározzuk az u-ból v-be vezető legrövidebb (legkisebb költségű) utat és ennek költségét a Floyd-Warshall algoritmus segítségével.
A gráfot egy éleket tartalmazó rendezett listával adjuk meg (DistGraph), amelynek élei (Edge) egy rendezett hármassal adottak. A rendezett hármas első két eleme egy-egy gráfbeli csúcs (Vertex) melyek pozitív egész értékek és a kezdő és a célcsúcsot adják meg, a harmadik érték pedig a csúcsok közötti él költsége/távolsága (Distance), amely egy tetszőleges egész érték.
Üres gráf létrehozása
Hozz létre egy üres gráfot, amely még nem tartalmaz éleket!
Új él hozzáadása a gráfhoz
Adjuk meg azt a műveletet, amely egy élet szúr be a gráfba! A gráf rendezett, ezért az él beszúrását az alábbi szabályok szerint kell elvégezni:
A gráf rendezett maradjon a beszúrás után.
A rendezést az első csúcs szerint, ha ezek megegyeznek, ezen belül a második szerint kell végezni.
Ha az adott két csúcs között még nincs él, akkor szúrd be az új élt.
Ha az adott két csúcs között van él, csak abban az esetben szúrd be az új élt, ha ez kisebb távolságú, mint a gráfban lévő.
A bevezetőben tárgyaltaknak megfelelően bevezetünk három konstanst, amely különböző gráfokat ír le:
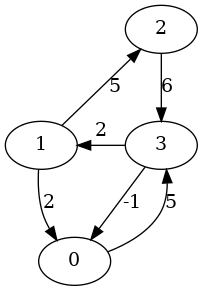
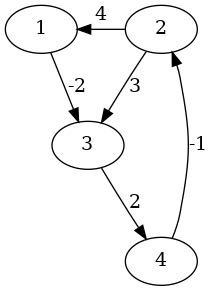
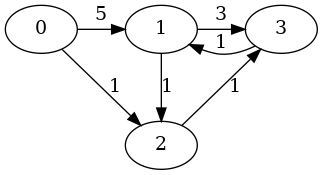
Végtelen érték
Bevezetünk egy infinity nevű konstanst, amely az Int típus maximális értékének felel meg.
Végtelen költségű-e?
Döntsd el, hogy egy távolság végtelen-e!
Él költsége
Definiáljuk azt a műveletet, amely megadja két csúcs távolságát egy gráfon belül! A függvény adjon vissza “végtelen” értéket, amennyiben a két csúcs között nincs közvetlen él.
Élköltségek összege
Add meg az összeadás műveletét a távolságokra! Ha az adott két távolság közül valamelyik végtelen, akkor az összeg is végtelen. Egyébként az eredmény legyen a két távolság összege.
Megjegyzés: Használd az isInfinity és infinity függvényeket!
Rövidebb út-e?
Döntsd el, hogy két csúcs a és b között a közvetlen út, vagy egy adott harmadik c csúcson át vezető kerülő út a kevésbé költséges.
A függvény első paramétere egy gráf, második paramétere egy kezdő- és célcsúcs pár (a, b) a harmadik paraméter pedig egy harmadik csúcs c. A függvény adjon vissza True értéket, ha a-ból olcsóbb b csúcsba jutni c csúcson keresztül, mint közvetlenül.
Megjegyzés: Használd a distance és addDistance függvényeket!
Az algoritmus az utak költségei mellett magukat az utakat is meghatározza. Ehhez egy új útvonalgráfot (PathGraph) vezetünk be. Hasonlóan az előző gráfhoz, ez is egy rendezett éleket (PathEdge) tartalmazó lista lesz. Az éleket rendezett hármasokkal adjuk meg, amely első két eleme a kiinduló és a célcsúcs, a harmadik pedig elem annak a csúcsnak a számát adja meg, amerre a legrövidebb út vezet.
Azaz, az (a, b, c) él azt írja le, hogy az a csúcsból a c csúcson keresztül kell indulni, hogy a legolcsóbb úton érjük el a b csúcsot.
Üres útvonalgráf létrehozása
Add meg azt a műveletet, amely létrehoz egy üres útvonalgráfot!
Amennyiben sikerül kisebb költségű utat találnunk, szükségünk lesz az útvonalgráf éleinek megváltoztatására, vagy kiegészítésére. A következő művelettel ezt fogjuk megadni.
Útvonalgráf megváltoztatása
Add meg azt a műveletet, amely egy új élet szúr be az útvonalgráfba, vagy egy létezőt módosít! Az útvonalgráf rendezett, ezért a megadásnál az alábbiakat vegyük figyelembe:
A gráf rendezett maradjon a beszúrás után.
A rendezést az első csúcs szerint, ha ezek megegyeznek, ezen belül a második szerint kell végezni.
Ha az adott két csúcs között még nincs él, akkor szúrd be az új élt.
Ha az adott két csúcs között van él, cseréljük ezt le az újra.
Útvonalgráf inicializálása
Definiáld azt a függvényt, amely egy kezdeti gráfból előállítja az útvonalgráfot! Minden gráfbeli csúcspárral, amennyiben van közöttük él, a köztes harmadik csúcs a célcsúcs legyen.
Van-e út?
Adjuk meg azt a függvényt, amely egy elkészített útvonalgráf és két csúcs megadásának segítségével eldönti, hogy létezik-e út a két csúcs között!
Haladási irány csúcs
Egy adott csúcspár (x, y) esetén adjuk meg az útvonalgráf segítségével, hogy melyik csúcs irányába kell elindulni az x kezdőcsúcsból, hogy a legrövidebb úton haladjunk csúcs y felé!
Ne felejtsük el ellenőrizni, hogy létezik-e út a két csúcs között. Amennyiben a kezdőcsúcsból elérhetetlen a célcsúcs, úgy az error függvény segítségével adjunk hibaüzenetet.
Jobb útvonal keresése
Adott egy távolságokat tartalmazó gráfból és egy útvonalgráfból álló pár, valamint egy kezdő és egy végpontból álló pár ((a, b)), és egy tetszőleges harmadik csúcs (c).
Adjuk meg azt a műveletet, amely ellenőrzi, hogy az a csúcsból b csúcsba kevésbé költséges-e eljutni c csúcson keresztül mint közvetlenül! Amennyiben ezen a harmadik csúcson át kisebb távolságú út van a kezdő csúcsból a cél csúcsba, ezen információval frissítsd a távolsággráfot. Az útvonalgráfban az a-ból b csúcsba vezető út iránya pedig az a-ból c csúcsba vezető út irányára változik. Ha a “kerülőútnak” nem kisebb a költsége, akkor az eredeti két gráfot add vissza.
Megjegyzés: Használd a korábbi függvényeket! (ensureEdge, changePathGraph, direction, distance)
Csúcsok listája
Add meg egy gráf összes csúcsát, legyen az kiinduló-, vagy célcsúcs! Az eredmény legyen rendezett és minden csúcsot csak egyszer tartalmazzon.
Floyd-Warshall egy lépése
Adjuk meg azt a függvényt, amely elvégzi az algoritmus egy lépését!
Ebben a lépésben azt vizsgáljuk meg az összes gráfbeli csúcspárra ((a, b)), hogy van-e a megadott csúcson (c) átvezető rövidebb út a-ból b-be.
Tehát adott egy távolsággráfból és egy útvonalgráfból álló pár, valamint egy csúcs (c). A gráf összes csúcspárjára, legyen ez i és j (amelyek egyike sem egyezik meg a vizsgált csúccsal, c ≠ i ∧ c ≠ j) megnézzük, hogy van-e jobb út az adott c csúcson keresztül és ez alapján módosíthatjuk a gráfokat (checkBetterPath).
Megjegyzés: Az eredménynek az összes felmerülő változtatást tartalmaznia kell!
Floyd-Warshall algoritmus
Definiáljuk a Floyd-Warshall algoritmusát megvalósító függvényt!
Az algoritmusnak a lépésszáma a gráfbeli csúcsok számától függ. Azaz, ha a gráfban i darab csúcs található, akkor az algoritmus i lépésben határozza meg a távolság- és az útvonalgráfokat.
Az algoritmus lépései:
Inicializáljuk egy útvonalgráfot a paraméterül kapott gráf felhasználásával .
Határozzuk meg a gráf csúcsait (
nodes).Vegyük az összes csúcsot a gráfból és alkalmazzuk a
stepműveletet mindegyik felhasználásával.
Megjegyzés: A gráfokat, mint állapotokat kezeljük, azaz a módosított gráfokat a következő lépésben fel kell használni.
Legjobb út
Adjuk meg a legrövidebb utat két csúcs között, az úton lévő csúcsok felsorolásával!
Bevezetünk egy útvonal (Path) szinonimát, amely csúcsok sorozatának felel meg:
Amennyiben létezik út a két megadott csúcs között, az útvonal az útvonalgráf bejárásával kapható meg. A megadott kezdőcsúcsból indulva követni kell az következő csúcsokat, amíg a célcsúcsba nem érkezünk. Ha nincs út a két megadott csúcs között, akkor adjunk vissza üres listát.
Az összes legjobb út
Adjuk meg az összes csúcspárra a köztük lévő legrövidebb utat az út költségével együtt!