A feladat összefoglaló leírása
A Piripócsi Tűzoltóság megbízott minket, hogy segítsük őket a felvonulási útvonalak megtervezésében. Az útvonal tervezésre egy leírást bocsátnak a rendelkezésünkre, amely tartalmazza az aktuálisan járható útszakaszokat.
A könnyebb feldolgozhatóság érdekében, a kapott leírásból készítettünk egy gráfot. A leírásban szereplő kereszteződéseket a gráf csúcsaiként (esetleg csomópontjaiként), a kereszteződéseket összekötő útszakaszok pedig a gráf éleiként fogjuk jelölni. Egyszerűsítésként, a gráf két csúcsa között megadott élek mindkét irányba járható útszakaszokat jelölnek (nincsenek egyirányú utak), illetve ezek egységnyi hosszúak. A feladat megoldása során feltételezhetjük, hogy a gráf összefüggő, azaz két tetszőlegesen kiválasztott csúcsa között létezik út.
A gráf reprezentációja
A gráfot (Graph) egy rendezett párok (Edge) listájával reprezentáljuk, a rendezett párok a gráf éleit adják meg. Egy rendezett pár (Edge) két csúcsból (Node) áll, amely a köztük lévő közvetlen utat adja meg. Ha egy (a,b) rendezett pár megtalálható a listában, ez mindkét irányú utat megadja, azt jelenti hogy az a-ból b-be és b-ből a-ba is át tudunk jutni.
(A type kulcsszó segítségével a gráf csúcsainak azonosítására használt Node típus az Int típus, a Edge típus a Node típusból képzett párok (Node, Node) típusának egy másik neve lesz. A Graph típus a Edge típusból alkotott listákat/sorozatokat fogja jelenteni, hasonlóan a String és [Char] viszonyához. A programban ez semmilyen további megszorítást nem indukál, csupán a beszédesebb függvénytípusok kialakításában segít.)
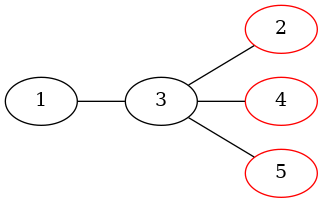
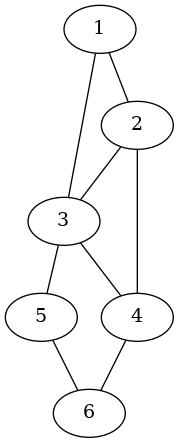
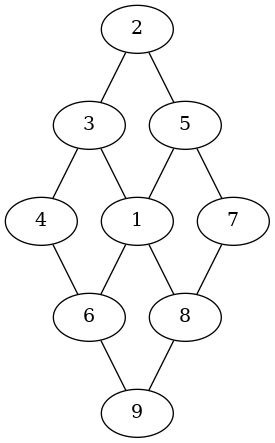
A megoldás teszteléséhez bevezetjük a következő három gráfot:
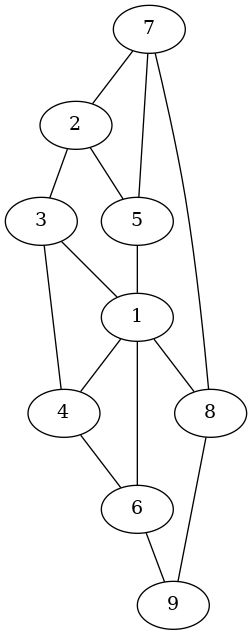
graph3 :: Graph
graph3 = [(7,2),(2,3),(3,4),(5,1),(1,6),(1,4),(7,8),(8,9),(2,5),(5,7),(3,1),(1,8),(4,6),(6,9),(9,8)]