Halmazkifejezések
- Halmazkifejezések
- Feladat: A 2 hatványai [*]
- Feladat: Az első 10 négyzetszám kétszerese
- Feladat:
False és True felváltva
- Feladat: Nagy 2 hatvány keresés [*]
- Feladat: 1024 > 1000, …
- Feladat: 60 osztói
- Feladat: 60 osztóinak száma
- Feladat: Prímvizsgálat [*]
- Párok
- Feladat: Órák és percek
- Feladat: Dominók [*]
- Feladat: ÉS és VAGY kötési erőssége
- Feladat: Hónapok és napok [*]
- Cipzározás
- Feladat: Sorszámozás [*]
- Feladatok végtelen listákkal
- Feladat: Az összes természetes számpár
- Feladat: 1, 2, 2, 3, 3, 3, … [*]
- Feladat: 1, 2, 1, 2, 3, 2, 1, … [*]
- Feladat: Csillagok [*]
- Feladat: Négyzetszámok elhagyása
- Feladat: 1,1,2,1,2,3,1,2,3,4,…
- Feladat: 0,1,0,-1,0,1,2,1,0,-1,-2,-1,0,1,2,3,2,1,0,-1,…
- Feladat: A π közelítése Leibniz-féle sorral
- Feladat: Számtani sorozatok keresése
Halmazkifejezések
Matematikai példakép: { n2 | n ∈ N, n páros }
Haskellben:
Feladat: A 2 hatványai [*]
Állítsuk elő a 2 hatványait növekvő sorrendben 1-től 210-ig!
Feladat: Az első 10 négyzetszám kétszerese
Soroljuk fel az első 10 négyzetszám kétszeresét!
Feladat: False és True felváltva
Állítsunk elő olyan 10 hosszúságú listát, amely váltakozva tartalmazza a False és True értékeket!
Feladat: Nagy 2 hatvány keresés [*]
Melyik legkisebb 2 hatvány nagyobb, mint 1020?
Megjegyzés: l !! 0 == head l.
Feladat: 1024 > 1000, …
Melyik legkisebb n természetes számra igaz: 1024n > 2 * 1000n?
Feladat: 60 osztói
Soroljuk fel a 60 osztóit!
Feladat: 60 osztóinak száma
Hány osztója van a 60-nak?
Feladat: Prímvizsgálat [*]
Prímszám-e az 123457?
Párok
A rendezett párok elemei lehetnek különböző típusúak:
Halmazkifejezés, amely párokat tartalmazó listát állít elő:
Feladat: Órák és percek
Állítsuk elő azt a listát, amely sorrendben tartalmazza az összes (óra, perc) párt!
Feladat: Dominók [*]
Állítsuk elő azt a listát, amely párként tartalmazza az összes dominót: [(0,0),(0,1),...,(0,9),(1,1),...,(9,9)]!
A (1,0) ne szerepeljen, mert az ugyanazt a dominót reprezentálja, mint a (0,1).
Megjegyzés: A dominók legkevesebb nulla, legtöbb kilenc pontot tartalmazhatnak.
Feladat: ÉS és VAGY kötési erőssége
Keressünk olyan a, b, c logikai értékeket, melyekre teljesül a következő logikai feltétel:
(a || (b && c)) /= ((a || b) && c)
Feladat: Hónapok és napok [*]
Állítsuk elő azt a listát, amely sorrendben tartalmazza az összes (hónap, nap) párt egy 365 napos évben!
Segítség: Használjuk az elem függvényt!
Cipzározás
Két listát az zip függvénnyel cipzározhatunk össze:
Megjegyzés: Ha valamelyik lista elfogy, a cipzározás véget ér.
Feladat: Sorszámozás [*]
Állítsuk elő az [(1,'a'),(2,'b'),…(…,'z')] listát!
Feladatok végtelen listákkal
Végtelen listák megnézésekor használjuk a take függvényt:
Mi a különbség?
Mi lesz ez?
Feladat: Az összes természetes számpár
Soroljuk fel a természetes számpárokat: [(0,0),(0,1),(1,0),(0,2),(1,1),(2,0), …]!
Feladat: 1, 2, 2, 3, 3, 3, … [*]
Állítsuk elő a következő listát: [1,2,2,3,3,3,4,4,4,4, …] ! Az i szám i-szer szerepel a listában.
Feladat: 1, 2, 1, 2, 3, 2, 1, … [*]
Próbáljuk ki a concat függvényt!
Állítsuk elő az 1,2,1,2,3,2,1,2,3,4,3,2,1,2,3,4,5,4,3,2,1,2,3,4,5,6,5,4,3,2,1,.. sorozatot!
Feladat: Csillagok [*]
Próbáljuk ki az unwords függvényt!
Állítsuk elő a következő végtelen szöveget: "* ** *** **** *****… !
Feladat: Négyzetszámok elhagyása
Állítsuk elő azt a listát, amelyet úgy kapunk, hogy a természetes számokból elhagyjuk a négyzetszámokat!
Feladat: 1,1,2,1,2,3,1,2,3,4,…
Állítsuk elő az [1,1,2,1,2,3,1,2,3,4,…] listát!
Feladat: 0,1,0,-1,0,1,2,1,0,-1,-2,-1,0,1,2,3,2,1,0,-1,…
Állítsuk elő a következő sorozatot: 0,1,0,-1,0,1,2,1,0,-1,-2,-1,0,1,2,3,2,1,0,-1, … !
Feladat: A π közelítése Leibniz-féle sorral
Írjunk olyan kifejezést, amely megadja π közelítő értékét a Leibniz-féle sor részleges előállításával! A képlet a következő:
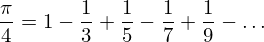
Természetesen ezt mi csak közelítjük, így elég az első ezer elem összegét venni, majd az eredményt néggyel megszorozni.
Segítség: Először érdemes az [1, -3, 5, -7, 9, -11, ... ] végtelen listát előállítani. Majd vegyük ezen elemek reciprokát és adjuk ezeket össze!
Feladat: Számtani sorozatok keresése
Tekintsük a következő egyenleteket:
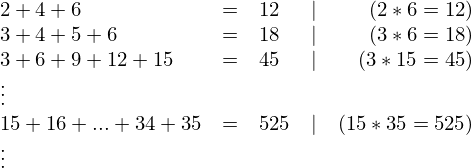
Az egyenletek bal oldalán olyan számtani sorozatok szerepelnek, amelyek összege egyenlő a sorozat első és utolsó elemének szorzatával.
Állítsuk elő az összes ilyen sorozatot, az utolsó elem nagysága szerint növekvő sorrendben!
Az ellenőrzéshez csak az első 6 sorozatot írjuk be.
Segítség: Használhatjuk a List modulban található init és tails függvényeket.