Feladat: Jobbra forgatás
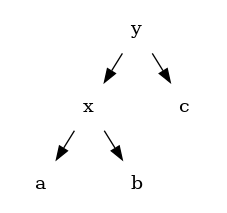
–>
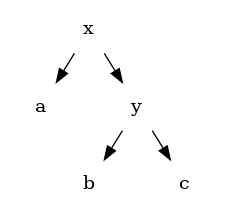
Tekintsük a következő adatszerkezetet (bináris fa):
Definiáljuk:
Definiáljuk:
Készítsünk egy 2 mélységű teljes fát készít 7 elemből!
Definiáljuk:
Definiáljuk:
Definiáljuk:
Rendezett fa (kersőfa): Minden csúcsra a bal oldali elemek kisebbek mint a csúcselem, a jobb oldaliak meg nagyobbak.
Segédfeladat: Állapítsuk meg egy listáról hogy rendezett-e!
Állapítsuk meg egy fáról hogy rendezett-e!
Definiáljuk:
Definiáljuk:
Egy fa kiegyensúlyozott, ha bármely részfájára a bal és jobb oldali részfa magasságkülönbsége legfeljebb 1.
AVL fa: Kiegyensúlyozott keresőfa
Magasság: A leghosszabb út hossza a fában.
Ferdeség: A bal és jobboldali részfák magasságának különbsége.
Kiegyensúlyozott fa: A ferdeség abszolút értéke <= 1, és minden részfája kigyensúlyozott.
A forgatások segítségével kicsit elbillent fát lehet kiegyensúlyozni.

–>


–>

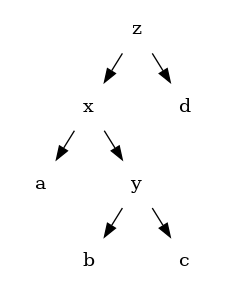
–>
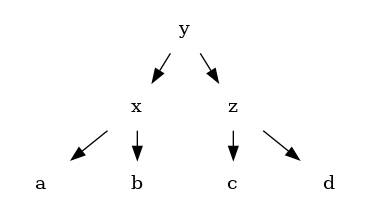
A kiegyensúlyozás művelete:
| feltétel | tennivaló |
|---|---|
| skew = 2, skew left = -1 | balra-jobbra forgatás |
| skew = 2 | jobbra forgatás |
| skew = -2, skew right = 1 | jobbra-balra forgatás |
| skew = -2 | balra forgatás |
| egyébként | semmi |
Ugyanaz, mint ins, de a rekurzív beszúrás után helyreállítjuk a kiegyensúlyozottságot.
sort :: Ord a => [a] -> [a]
-- inorder, listToTree
listToTree :: Ord a => [a] -> T a
-- foldr, balInsKészítsünk egy másolatot a forráskódról.
A fa magasságát tároljuk el az algebrai adattípusban:
“smart” konstruktor és módosított height: